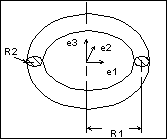
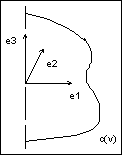
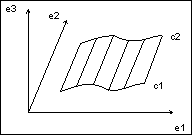
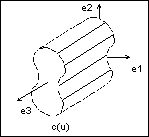
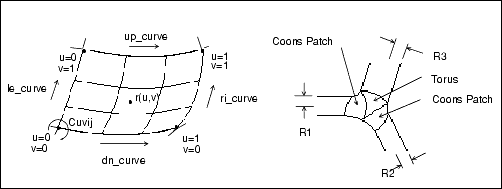
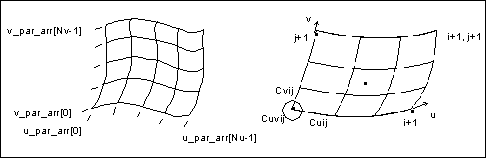
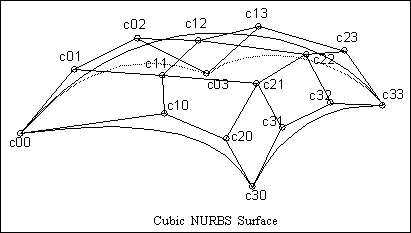
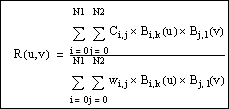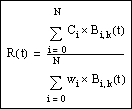Domain of Evaluation
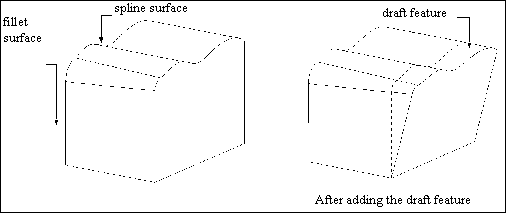
Surfaces and edges can be extended from their original domain as the user continues to add features to the model. For example,
the user can add a feature such as a draft surface or local push, which requires the original surface to be extended outside
its original domain.
When this occurs, you will find that the uv parameters of the surface have been extended. The ProSurfacedata data structure reflects the extension, and returns the updated values for the u and v extents.
Because the evaluator functions use the analytical surface (or curve) definition, they work for any parameter values. Thus,
any surface (or curve) can be extended as needed. In addition, if you pass in parameters outside the current uv domain, the evaluator functions still return values for the parameters as requested.
If you are using the evaluators supplied by Creo TOOLKIT, you do not have to do anything. For surfaces, the evaluator functions work over this extended range of parameters. Your
evaluator function for foreign datum surfaces is also expected to allow for extrapolation.
Edges are always parameterized between 0.0 and 1.0. When surfaces are extended, new edges are created that have parameters in the range 0.0 to 1.0.
If you develop your own evaluator functions, you must be aware that the domain of a surface can be extended, as with foreign
datum surfaces.
Surfaces